A SIN Excel függvény egy beépített trigonometrikus függvény az excelben, amelyet az adott szám szinuszértékének vagy trigonometria szempontjából egy adott szög szinuszértékének kiszámítására használunk, itt a szög egy szám az excelben, és ez a függvény csak egyetlen argumentumot vesz igénybe amely a megadott bemeneti szám.

SIN funkció az Excelben

Az SIN függvény az Excelben kiszámítja az általunk megadott szög szinuszát. A SIN in Excel függvény matematikai / trigonometriai függvényként van besorolva az Excel programban. A SIN az excelben mindig számértéket ad vissza.

A matematikában és a trigonometriában a SINE egy szög trigonometrikus függvénye, amely egy derékszögű háromszögben egyenlő az ellenkező oldal (a derékszögű oldal) hosszával, elosztva a hipotenusz hosszával, és ezt :

Sin Θ = ellentétes oldal / hipotenusz

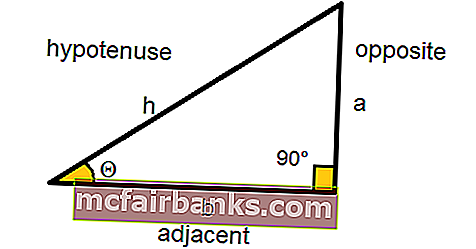
Sin Θ = a / h

SIN formula az Excelben

Az alábbiakban látható az SIN-formula az Excel-ben.

Ahol a SIN képletnek radiánban megadott argumentuma van.

Ha a szöget közvetlenül átadjuk a SIN-nek az excel függvényben, akkor nem fogja érvényes argumentumként felismerni. Például, ha 30 ° -ot adunk át argumentumként ennek a SIN-nek az Excel-függvényben, akkor nem ismeri el érvényes argumentumnak. Az Excel hibaüzenetet jelenít meg.

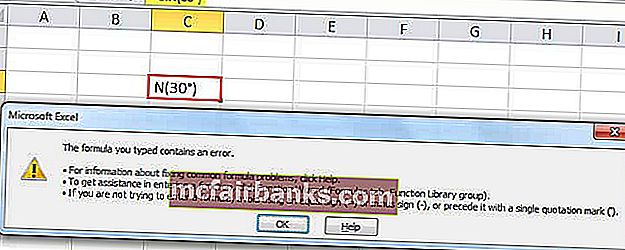
Ezért az érvnek, amelyet át kell adnunk, radiánban kell megadni .

A szög radiánvá alakításához két módszer létezik

1. Használja a beépített Excel RADIANS funkciót. A RADIANS függvény a fokokat radián értékre konvertálja.

Például a 30 ° radiánra konvertálásához ezt a funkciót fogjuk használni, a fokot számként veszi, a 30 ° -ot pedig 30-ként.

= RADIÁNOK (30) a radiánt 0,52-nek adják

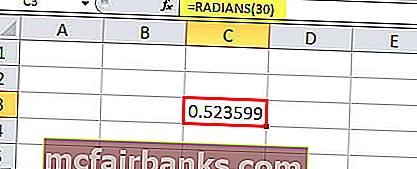
2. A második esetben a matematikai képletet használhatjuk egy fok radiánra konvertálásához. A Formula az

Radián = fok * (π / 180) (π = 3,14)

Az excelben van egy olyan függvénye is, amely visszaadja a Pi értékét, 15 számjegyre pontos, és a függvény PI ()

Ezért a fok-radián átváltáshoz a képletet használnánk

Radián = fok * (PI () / 180)

Hogyan kell használni a SIN funkciót az Excelben?

A SIN funkció az Excelben nagyon egyszerű és könnyen használható. Néhány példával ismerje meg a SIN működését az excelben.

Itt töltheti le ezt a SIN-t az Excel-sablonban - a SIN-t az Excel-sablonban

BŰN az Excel 1. példában

A szinuszérték kiszámítása az SIN függvény használatával az Excelben és a RADIANS függvény használata az Excel programban

A szinuszérték kiszámítása az SIN függvény használatával az Excelben és a PI függvényben

Az Excel szinuszfüggvénye számos valós alkalmazással rendelkezik; széles körben használják az architektúrákban a geometriai ábrák magasságának és hosszának kiszámításához. GPS-ben, optikában, a pályák kiszámításakor is használják, hogy megtalálják a legrövidebb útvonalat a földrajzi szélesség és hosszúság földrajzi elhelyezkedése, rádiós műsorszórás stb. Alapján. Még egy elektromágneses hullám is ábrázolásra kerül a szinusz és a koszinusz függvény grafikonjaként.

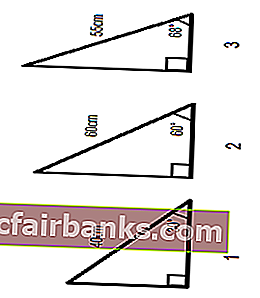
Tegyük fel, hogy három derékszögű háromszögünk van, az egyik oldal szöge és hossza megadva, és ki kell számolnunk a másik két oldal hosszát.

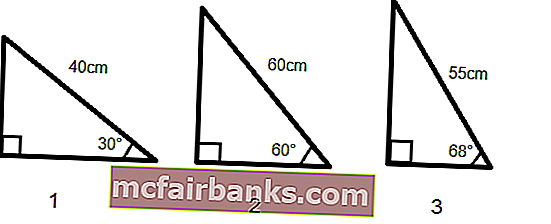
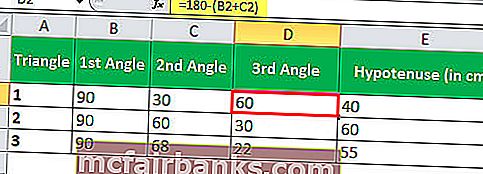
A háromszög összes szögének összege 180 °, ezért könnyen kiszámíthatjuk a harmadik szöget.

Tudjuk, Sin Θ = ellentétes / hipotenusz

Tehát az ellenkező oldalhosszúság Sin Θ * hipotenusz lesz

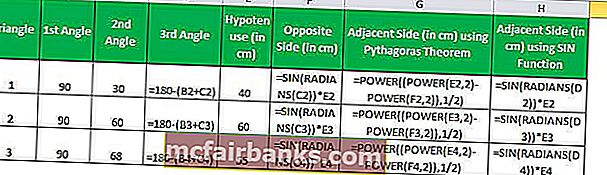
Az Excelben az ellentétes oldal (merőleges oldal) hosszát a SIN képlettel kell kiszámítani

= BŰN (RADIÁNOK (C2)) * E2

A fenti SIN képletet három háromszögre alkalmazva megkapjuk a háromszögek merőlegeseinek hosszát

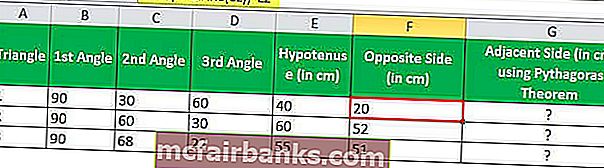
A harmadik oldalra (a szomszédos oldalra) két módszerünk van - Pythagoras-tétel vagy ismételten a SIN in Excel funkció más szögekből történő felhasználásával.

A Pythagoras-tétel szerint a derékszögű háromszög két oldalának négyzetösszege egyenértékű a hipotenusz négyzetével.

Hypotenuse2 = szemben2 + szomszédos2

Szomszédos = (Hypotenuse2 - szemben 2) 1/2

Az Excelben ezt fogjuk írni,

= POWER ((POWER (Hypotenuse, 2) -POWER (szemben, 2)), 1/2)

Ezen képlet alkalmazásával kiszámoljuk a szomszédos oldal hosszát

= POWER ((POWER (E2,2) -POWER (F2,2)), 1/2)

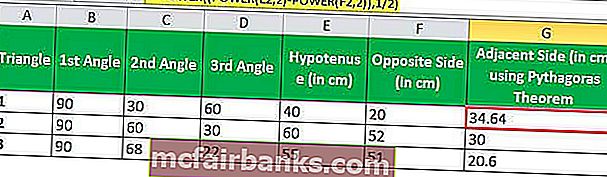
A második módszer segítségével a 3. szög SINE-jét használhatjuk a szomszédos oldal értékének kiszámításához

Ha a háromszögeket 90 ° -kal balra forgatjuk, akkor az ellenkező oldalt felcseréljük a szomszédos oldalra, és a hipotenusz és a szomszéd közötti szög SIN-je segít kiszámítani a harmadik oldal értékét.

= BŰN (RADIÁNOK (D2)) * E2

SIN az Excel 2. példájában

Van egy magas, ismeretlen magasságú épület, és a napsugár egy adott időpontban az A pontban 75 ° -os szöget zár be, így a 70 méter hosszú épület árnyéka lesz. Meg kell találnunk a torony magasságát

Az épület magasságát a SIN in excel függvényben kell kiszámítani

SIN 75 ° = Épületmagasság / Árnyékhossz az A pontban

Ezért az épület magassága = SIN 75 ° * Az árnyék hossza az A pontban

Ennélfogva az épület magassága lesz

= BŰN (RADIÁNOK (B3)) * B2

Az épület magassága 67,61 méter

SIN az Excel 3. példájában

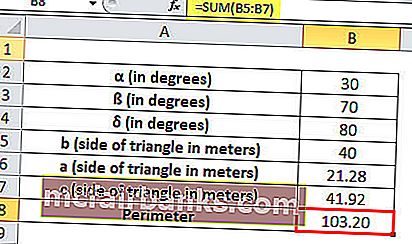
Van egy földünk háromszög alakjában, amelyre a két szöget 30 ° -nak és 70 ° -nak adjuk meg, és csak a háromszög egyik oldalának hosszát ismerjük, amely 40 méter. Meg kell találnunk a másik három oldal hosszát és a háromszög kerületét.

Egy háromszög esetében, ha az egyik oldal és az összes szög ismert, a többi oldalát SINE szabály alapján számíthatjuk ki

A trigonometriai szinusz-szabály összefüggést ad a háromszög sin szögeivel és oldalaival egy SIN képlettel

a / sin α = b / sin ß = c / sin δ

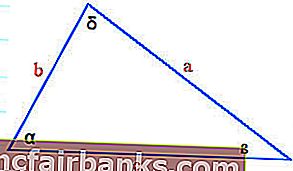
Ebben az esetben,

α = 30 °, ß = 70 ° és δ = 180 ° - (30 ° + 70 °) = 80 ° és a b háromszög egyik oldala = 40 méter

A háromszög többi oldalának megtalálásához a SINE szabályt fogjuk használni

a = Sin α * (b / sin ß)

Ezért,

a = BŰN (RADIÁNOK (30)) * (B5 / BŰN (RÁDIÁNOK (70)))

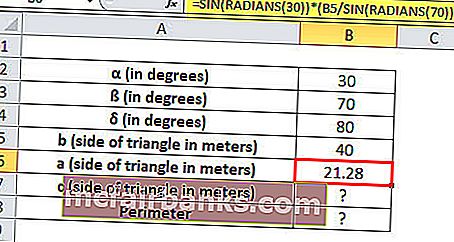
Az a oldal hossza = 21,28 méter

Hasonlóképpen a c harmadik oldal is

c = Sin δ * (b / sin ß)

Ezért,

c = BŰN (RADIÁNOK (80)) * (B5 / BŰN (RÁDIÁNOK (70)))

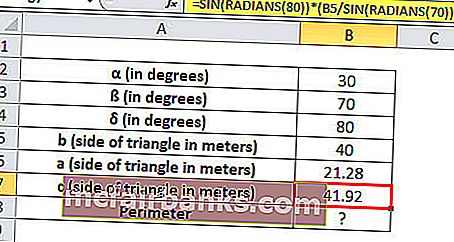
A háromszög három oldala 21,28, 40, 41,92 méter hosszú.

A háromszög kerülete az összes oldal összege.

Ezért a kerülete = SUM (B5: B7) lesz