Sharpe arány meghatározása
A Sharpe arány William F. Sharpe által kidolgozott és a befektetők által a portfólió volatilitási (szórás) egységére jutó, a hozam kockázatmentes hozamát meghaladó átlagos hozamának kiszámításához használt arány a befektetők által.
Magyarázat
A Sharpe Ratio kritikus elem a portfólió teljes megtérülésének jelölésében. Ez az átlagos hozam, amely meghaladja a kockázatmentes hozamot a viselt kockázat teljes összegéhez viszonyítva. Ez egy módja annak, hogy megvizsgáljuk a befektetés teljesítményét azáltal, hogy kiigazítjuk annak kockázati összetevőjét. A Sharpe arány jellemzi, hogy egy eszköz megtérülése mennyiben kompenzálja a befektetőt a vállalt kockázatért. Ha két eszközt összehasonlítunk egy közös referenciaértékkel, akkor a magasabb Sharpe-aránnyal bíró eszközt kedvező befektetési lehetőségként jelölik ugyanazon kockázati szinten.
Ha megnézi a fenti táblázatot, látni fogja, hogy a PRWCX magasabb Sharpe Rátával, 1,48-zal rendelkezik, és a legjobb alap a csoportjában.
A Sharpe Ratio, mint bármely más matematikai modell, a helyes adatoknak a pontosságára támaszkodik. Az eszközök befektetési teljesítményének a megtérülés simításával történő vizsgálata során a Sharpe-arányt az alapok hozama helyett az alapul szolgáló eszközök teljesítményéből származtatnák. Ezt az arányt, a Treynor arányokkal és Jeson Alfáival együtt gyakran használják a különböző portfóliók vagy alapkezelők teljesítményének rangsorolására.
Képlet
1966-ban William Sharpe kifejlesztette ezt az arányt, amelyet eredetileg „jutalom-változó” aránynak nevezték, mielőtt a későbbi tudósok és pénzügyi szereplők Sharpe-aránynak nevezték volna. Többféle módon definiálták, míg végül az alábbiak szerint ábrázolták:
Sharpe Ratio képlet = (Várható hozam - kockázatmentes megtérülési ráta) / szórás (volatilitás)
Néhány fogalom, amelyet meg kell értenünk:
- Visszatérések - A hozamok különböző gyakoriságúak lehetnek, például napi, heti, havi vagy éves, mindaddig, amíg az eloszlás normálisan eloszlik, mivel ezeket a hozamokat éves szinten lehet pontos eredmények elérése érdekében. Az olyan kóros helyzetek, mint a magasabb csúcsok, az eloszlás torzulása problémát jelenthet az arány szempontjából, mivel a szórásnak nincs ugyanolyan hatékonysága, ha ezek a kérdések fennállnak.
- Kockázat nélküli megtérülési ráta - Ezt használják annak felmérésére, hogy az embert helyesen kompenzálják-e a kockázatos eszköz miatt viselt további kockázatért. Hagyományosan a pénzügyi veszteség nélküli megtérülési ráta a legrövidebb időtartamú állampapír (pl. Amerikai kincstárjegy). Bár az értékpapír ilyen változatának volatilitása a legkevesebb, vitatható, hogy az ilyen értékpapíroknak meg kell egyezniük más, azonos időtartamú értékpapírokkal.
- Szórás - Ez egy olyan mennyiség, amely kifejezi, hogy egy adott változóhalmaz hány egysége különbözik a csoport Átlagos átlagától. Miután kiszámították ezt a többlethozamot a kockázatmentes hozam felett, el kell osztani a mérendő kockázatos eszköz szórásával. Nagyobb szám, vonzóbb lesz a befektetés kockázat / megtérülés szempontjából. Mindazonáltal, kivéve, ha a szórás lényegesen nagy, a tőkeáttétel-komponens nem befolyásolhatja az arányt. A számláló (visszatérés) és a nevező (szórás) problémamentesen megduplázható.
Példa
Az „A” ügyfél jelenleg 450 000 dollárt tart befektetve egy portfólióban, várható hozama 12%, volatilitása 10%. A hatékony portfólió várható hozama 17%, volatilitása 12%. A kockázatmentes kamatláb 5%. Mi a Sharpe arány?
Sharpe Ratio képlet = (Várható hozam - kockázatmentes megtérülési ráta) / szórás (volatilitás)
Sharpe arány = (0,12-0,05) / 0,10 = 70% vagy 0,7x
Sharpe arány kiszámítása az Excelben
Most, hogy tudjuk, hogyan működik a képlet, számítsuk ki a Sharpe arányt excelben.
1. lépés - A hozamokat táblázatos formátumban kapja meg
Az első lépés az elemezni kívánt befektetési alap portfóliójának hozamának megszervezése. Az időszak lehet havi, negyedéves vagy éves. Az alábbi táblázat a befektetési alap éves hozamát mutatja be.
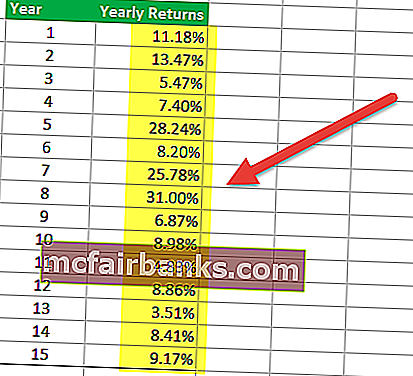
2. lépés - A kockázatmentes hozam részleteinek megismerése a táblázatban
Az alábbi táblázatban feltételeztem, hogy a kockázatmentes hozam 3,0% az egész 15 év alatt. A kockázatmentes kamatláb azonban évente változhat, és ezt a számot ide kell tennie.
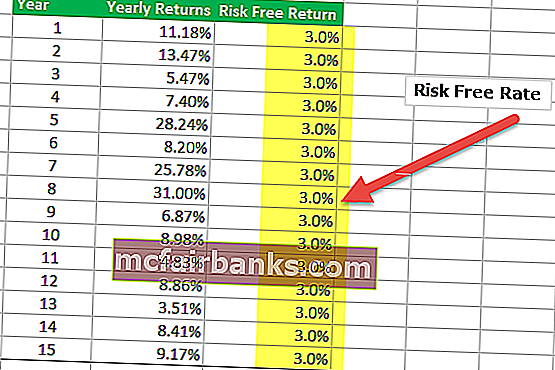
3. lépés - Keresse meg a felesleges hozamot
A Sharpe arány excelben történő kiszámításának harmadik lépése a portfólió többlethozamának megállapítása. Esetünkben a többlethozam az éves hozam - kockázatmentes megtérülés.
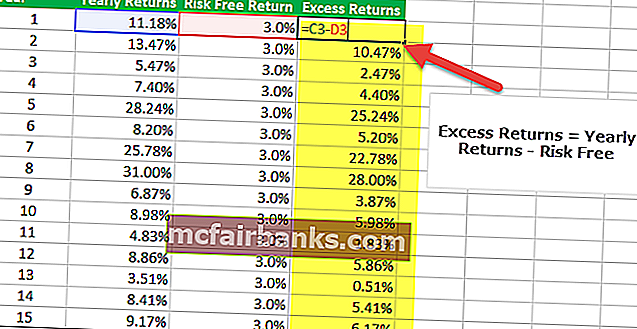
4. lépés - Keresse meg az éves hozam átlagát.
A Sharpe arány kiszámításának negyedik lépése az excelben az éves hozam átlagának megkeresése. Az ÁTLAGOS excel képlet segítségével megkeresheti a portfólió átlagát. Példánkban átlagosan 12,09% -os hozamot kapunk.
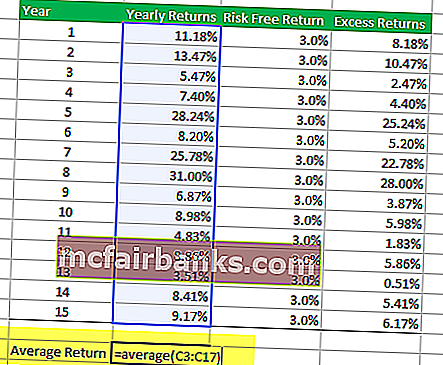
5. lépés - Keresse meg a felesleges hozamok szórását
A többlethozamok szórásának megtalálásához használhatja az alábbiakban megadott excel STDEV képletet.
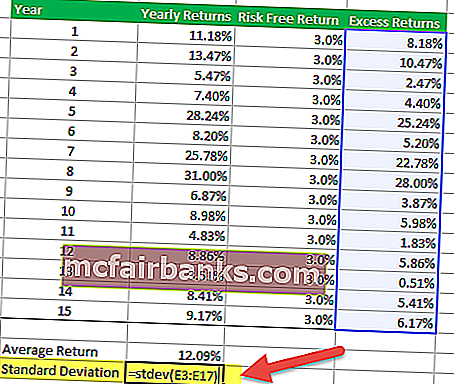
6. lépés - Számítsa ki a Sharpe arányt
A Sharpe arány excelben történő kiszámításának utolsó lépése az átlagos hozamok elosztása a szórással. Megkapjuk az arányt = 12,09% / 8,8% = 1,37x
Megkapjuk az arányt = 12,09% / 8,8% = 1,37x

A Sharpe Ratio használatának előnyei
# 1 - A Sharpe Ratio segít az új eszközök hozzáadásának összehasonlításában és szembeállításában
Arra használják, hogy összehasonlítsák a portfólió általános kockázat-hozam jellemzőinek szórását, amikor új eszközt vagy eszközosztályt adnak hozzá.
- Például egy portfóliókezelő fontolóra veszi egy alapanyag-allokáció hozzáadását meglévő 80/20-as befektetési portfóliójához, amelynek Sharpe-mutatója 0,81.
- Ha az új portfólió felosztása 40/40/20 részvények, kötvények és adósságalapok felosztása, akkor a Sharpe arány 0,92-re nő.
Ez azt jelzi, hogy bár az árupénztári befektetések önálló kitettségként volatilisak, ebben az esetben ez valóban a kombinált portfólió kockázat-hozam jellegzetességének javulásához vezet, és ezáltal egy másik eszköz diverzifikációjának előnye. osztály a meglévő portfólióhoz. Gondos elemzésnek kell részt vennie abban, hogy az alapok felosztását később módosítani kell, ha ez negatív hatással van a portfólió állapotára. Ha az új befektetés hozzáadása az arány csökkenéséhez vezet, akkor azt nem szabad szerepeltetni a portfólióban.
# 2 - A Sharpe Ratio segít a kockázat-hozam összehasonlításban
Ez az arány útmutatást adhat arra vonatkozóan is, hogy a portfólió túlzott hozama a befektetési alapos gondos döntéshozatal vagy indokolatlan kockázatok következménye. Annak ellenére, hogy egy egyéni alap vagy portfólió nagyobb hozamot élvezhet, mint társai, ez csak ésszerű befektetés, ha ezek a magasabb hozamok nem járnak indokolatlan kockázatokkal. Minél nagyobb a portfólió Sharpe aránya, annál jobb a teljesítménye a kockázati összetevőt. A negatív Sharpe arány azt jelzi, hogy a kevésbé kockázatos eszköz jobban teljesítene, mint az elemzett értékpapír.
Vegyünk egy példát a kockázat-hozam összehasonlításra.
Tegyük fel, hogy az A portfólió 12% -os megtérülési rátával rendelkezik vagy várható, 0,15 szórással. Körülbelül 1,5% -os referencia-hozamot feltételezve a megtérülési ráta (R) 0,12, Rf 0,015 és 's' 0,15. Az arány (0,12 - 0,015) / 0,15, amely 0,70-re számol. Ennek a számnak azonban akkor lesz értelme, ha összehasonlítjuk egy másik portfólióval, mondjuk a „B” portfólióval
Ha a „B” portfólió nagyobb változatosságot mutat, mint az „A” portfólió, de ugyanolyan megtérülést mutat, akkor nagyobb lesz a szórása, azonos megtérülési rátával a portfóliótól. Feltételezve, hogy a B portfólió szórása 0,20, az egyenlet (0,12 - 0,015) / 0,15. Ennek a portfóliónak a Sharpe-mutatója 0,53 lesz, ami alacsonyabb az „A” portfólióhoz képest. Ez nem biztos, hogy megdöbbentő eredmény, figyelembe véve azt a tényt, hogy mindkét beruházás ugyanazt a hozamot nyújtotta, de a „B” -nek nagyobb volt a kockázata. Nyilvánvalóan előnyben részesítendő az, amelynek kisebb a kockázata, hogy ugyanazt a hozamot kínálja.
A Sharpe Ratio kritikája
A Sharpe-arány a nevezőben a hozamok szórását használja a teljes portfólió-kockázat alternatívájaként, azzal a feltételezéssel, hogy a hozamok egyenletesen oszlanak meg. A korábbi tesztek azt mutatták, hogy bizonyos pénzügyi eszközök hozama eltérhet a normál elosztástól, ami a Sharpe-arány releváns értelmezését tévesen eredményezheti.
Ezt az arányt különböző alapkezelők javíthatják, ha megpróbálják növelni látszólagos, kockázattal korrigált hozamukat, amely az alábbiak szerint hajtható végre:
- A mérendő időtartam növelése : Ez kisebb volatilitási valószínűséget eredményez. Például a napi hozam évesített szórása általában magasabb, mint a heti hozam, ami viszont magasabb, mint a havi hozamé. Nagyobb időtartam, tisztább kép ki kell zárnia minden olyan egyszeri tényezőt, amely befolyásolhatja az általános teljesítményt.
- A havi hozamok összevonása, de a szórás kiszámítása, kivéve ezt a nemrégiben kiszámított összesített havi hozamot.
- Portfólió pénz nélküli eladási és vételi döntéseinek megírása: Egy ilyen stratégia potenciálisan növelheti a hozamot azáltal, hogy az opciós prémiumot beszedve éveken át nem térül meg. Az alapértelmezett kockázat, a likviditási kockázat vagy más, széles körben elterjedt kockázatok megkérdőjelezésével járó stratégiák ugyanúgy képesek felfelé elfogult Sharpe-arányt jelenteni.
- A hozamok simulása: Bizonyos derivatív struktúrák, a kevésbé likvid eszközök piacon történő szabálytalan megjelölése vagy bizonyos árképzési modellek alkalmazása, amelyek alábecsülik a havi nyereséget vagy veszteséget, csökkenthetik a várható volatilitást.
- Az extrém hozamok kiküszöbölése: A túl magas vagy alacsony hozam növelheti bármely portfólió jelentett szórását, mivel ez az átlagtól való távolság. Ilyen esetben az alapkezelő dönthet úgy, hogy minden évben kiküszöböli a havi legszélső (legjobb és legrosszabb) hozamokat a szórás csökkentése és az eredmények befolyásolása érdekében, mivel egy ilyen egyszeri helyzet befolyásolhatja a teljes átlagot.
Ex-Ante és Ex-Post Sharpe arány
A Sharpe arányt többször felülvizsgálták, de két általános formát használtak: az előzetes (a jövedelem és a variancia előrejelzése) és az utólagos (a múltbeli hozamvariancia elemzése).
- Az előzetes Sharpe arány- előrejelzések egyszerűbben becsülhetik meg a mintákat a hasonló befektetési tevékenységek múltbeli teljesítményének megfigyelését követően.
- Az utólagos Sharpe Ratio azt méri, hogy mekkora volt a hozam, szemben azzal, hogy ezek a hozamok mennyire változtak egy adott időszakban. Pontosabban, ez a különbözõ hozamok (a befektetés megtérülése és a benchmark befektetés közötti különbség) és a hozamok korábbi változékonysága (szórás) aránya.
Következtetés
A Sharpe arány a portfólió teljesítményének szokásos mértéke. Egyszerűségének és egyszerű értelmezésének köszönhetően az egyik legnépszerűbb index. Sajnos a felhasználók többsége megfeledkezik azokról a feltételezésekről, amelyek nem megfelelő eredményt eredményeznek. A piaci döntés meghozatala előtt fontolóra kell vennie a hozamok eloszlásának ellenőrzését vagy az eredmények validálását egyenértékű teljesítménymutatókkal.